Deuxième article de notre dossier sur la maîtrise de l’appareil photo réflex. Il traite aujourd’hui d’un réglage qui influe à la fois sur l’exposition et sur la profondeur de champs, l’ouverture

L’ouverture

L’ouverture représente le diamètre du trou par lequel passe la lumière, donc la surface du cercle qui modélise le passage du flux dans l’objectif.

Le terme exact qui définit l’ouverture est le ‘diaph’, abréviation de diaphragme. C’est un rapport (il n’a donc pas d’unité) et se note f. Par exemple, on dit donc ‘tu es à quel diaph? f:5,6 (phonétiquement : f cinq six)

f = longueur focale / diamètre ouverture

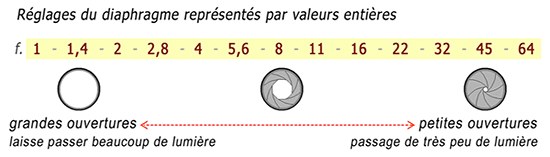
A chaque changement de valeur de diaph NORMALISEE (qui suit la progression d’une suite géométrique de raison √2), on divise/multiplie la quantité de lumière incidente par 2. Il vous faut absolument connaitre ces valeurs normalisées par coeur:

1
1,4
2
2,8
4
5,6
8
11
16
22
32

Les plus observateurs noteront qu’un nombre sur deux est le double de son suivant.

PLUS F EST PETIT, PLUS L’OUVERTURE DU DIAPHRAGME EST GRANDE

© creajcc.over-blog.com

En théorie, si l’environnement est sombre, on ‘ouvre’ (f petit) et si l’environnement est lumineux, on ‘ferme’. En réalité ce n’est pas vrai car la valeur de diaph influe sur la profondeur de champ. La profondeur de champ, c’est ce qui sera net. De manière plus subtile, c’est choisir un point (faire le point) à partir duquel tout est net en amont ou en aval. Plus on ouvre, plus il y a de lumière, plus il est difficile de différencier les plans, donc on détache le personnage du premier plan.

CE SCHÉMA EST TRES SIMPLIFIE ET NE TIENT PAS COMPTE DE LECHELLE DE CALCUL DE LA PROFONDEUR DE CHAMP. CELA SERA ELABORE AVEC PLUS DE DETAILS DANS UN PROCHAIN ARTICLE.

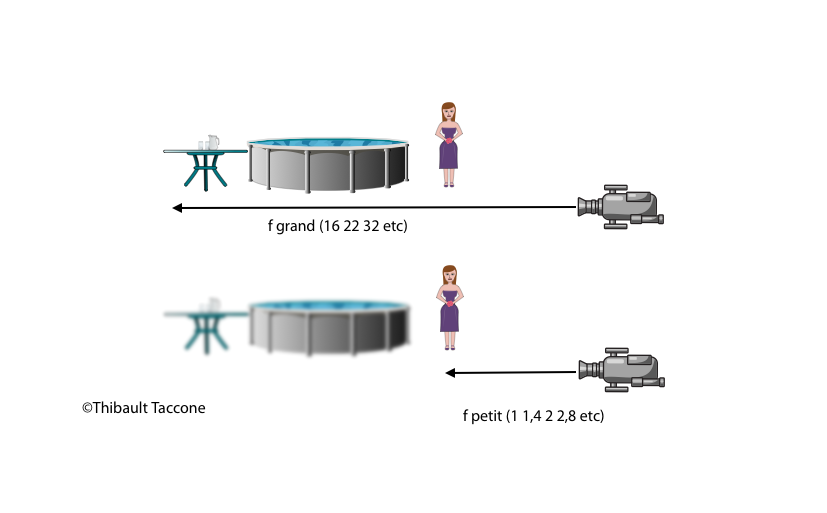
Si votre choix artistique est d’avoir une très grande profondeur de champ, vous devrez impérativement fermer. Cependant, vous aurez moins de lumière, alors que fait-on ? On laisse passer la lumière plus longtemps.

Pour aller plus loin

Il existe aussi des valeurs non normalisées, qui sont « les tiers de diaph ». Il y a donc entre chaque valeur normalisée deux valeurs qui sont respectivement f+1/3 et f+2/3 (f+3/3 = f+1 correspondant à une incrémentation, donc à un pas dans la suite). Certains boîtiers offrent la possibilité de travailler au 10ème de diaph ce qui est totalement inutile car l’oeil n’est pas assez sensible à ces variations d’intensité. Mais il parait que certains y trouvent leur compte alors on ne va pas chipoter.

Sachez qu’au 1/3 de diaph près, le point se joue à 2 cm près. C’est à dire que si vous vous réglez à f:1+1/3 (f:1,12), vos modèles ont une marge de manoeuvre de 2cm sur l’axe z avant d’être flous. Cette valeur est générique bien sûr et dépend de votre optique, mais c’est pour dire que pinailler pour avoir THE diaph, a aussi une contrainte physique. Il faudra donc imposer une pose statique pour ne pas flouter. En paysage, si bon vous semble, callez vous à f:12,70 !

Pour ceux et celles qui veulent savoir comment se passe l’ajout des tiers de diaph, voici l’explication.

On sait qu’entre chaque valeur normalisée, il y a un facteur √2.
En effet, le diaphragme est modélisé par un cercle dont la surface est S = π.r2
Notre but est de doubler la quantité de lumière entre chaque changement normalisé de diaph, donc de doubler la surface du cercle.

Si r = 1 => S = π.1.1 = π
Si r = 2 => S = π.2.2 = 4 π

En doublant le rayon, on multiplie par 4 la surface (ce qui est logique puisque l’on a un rapport de puissance de 2). Pour que la surface soit multipliée par 2, il faut que r2= 2 donc r = √2

On peut le vérifier facilement

Si r = 1 => S = π.1.1 = π
Si r = √2 => S = π(√2)² = 2π
Si r = √2.√2 = 2 => S = π2² = 4π
Si r = 2√2 => S = π(2√2)² = π.4.2 = 8π

Pour doubler la surface, il faut multiplier le rayon par √2, réel constant non nul. Comme on est en physique, on admet qu’il ne peut pas y avoir de chiffre nul donc Un > 0. On a affaire à une suite géométrique de forme Un+1 / Un = q avec q = √2 et U0 = 1
Pourquoi 1 ? Comme la suite représente les valeurs de f, on ne peut pas aller en dessous de 1 (par exemple: 0,5) car 1 représente l’ouverture maximale, c’est à dire lorsque le diaphragme est complètement ouvert.

NB: augmenter le rayon revient à « augmenter le cercle », et donc à ouvrir, c’est à dire se rapprocher de f:1 ou f:1,4.
Même si les valeurs 1, 1,4, 2, 2,8 sont les mêmes que celles de f, on parle ici de RAYON et PAS DE DIAPH.

CALCUL DES VALEURS NORMALISEES DE DIAPH:

Un+1 = q Un
U0 = 1
U1 = 1.q = √2 = 1,4 (arrondi)
U2 = 1,4 (arrondi précédent).q = 1,4. √2 = 2
U3 = 2√2 = 2,8
etc.

Magique non ?

Comme la suite est géométrique, on calcule le énième terme de la façon suivante: Un = U0.q(n-1)
Comme U0 = 1, le énième terme équivaut en fait à q(n-1) = qi
Pour les tiers de diaph, on les calcule de la manière suivante: qi+(1/3) et qi+(2/3) où i = indice d’ouverture.

Mais d’où ça sort ?

i représente le nombre d’incrémentation, c’est à dire le nombre de fois où l’on a changé de diaph. On est obligé de prendre en compte ce paramètre car si la suite commence avec un premier terme, pour nous, physiquement, cela représente le point de départ mais le processus que nous sommes en train d’étudier, à savoir le changement de diaph (dans cet ordre là, la fermeture) n’a « pas encore débuté », donc il est à 0. Ce qui fait que:

A U0, i = 0 (car « on est au premier terme »)
Si à U0, i = 0, en revanche n = 1 (car il représente le nombre de termes)
donc i = n-1

Si l’on se place à u1 qui est le 2ème terme
On a vu plus haut qu’il vaut U1 = 1.q = √2
On sait aussi que
q(n-1) = Un
Donc
q(2-1) = q1 = √2

Donc, à u1 qui est le second terme, on a fait UN SEUL changement de diaph (pour passer du premier au second terme), donc i = 1
Du coup, on a :
qi = q1 = √2
q(1+1/3) = q(4/3) = √21,3
q(1+2/3) = q(5/3)= √21,7

L’important n’est pas le résultat mais de savoir comment on incrémente d’un tiers de diaph.